Heeft u zich ooit afgevraagd of uw beleggingen het goed doen vanwege uw goede investeringsbeslissingen of omdat u een te hoog risico neemt? Om die vraag te beantwoorden, hebben we een methode nodig om de prestaties van verschillende portefeuilles te vergelijken die ook rekening houdt met hun risiconiveau. Dit is waar het bij "risicogecorrigeerde rendementen" om draait.
Waarschijnlijk de bekendste manier om voor risico gecorrigeerde rendementen te meten, is de Sharpe-ratio, die is ontwikkeld door de Nobelprijswinnaar econoom William Sharpe. Het wordt berekend door het 'excessrendement' van uw portefeuille voor een bepaalde periode te bepalen en dat vervolgens te delen door de standaarddeviatie van de portefeuille, wat een maatstaf is voor het volatiliteitsrisico.
Het extra rendement van uw portefeuille is het bedrag dat het verdiende boven het rendement van een risicovrij actief, meestal een kortlopende Amerikaanse staatsobligatie. Dus als de obligatie 3% rente betaalt en uw portefeuille 5% verdient, dan is uw extra rendement 2%.
We zullen in de volgende sectie ingaan op de details, maar het belangrijkste punt om in gedachten te houden is dit:de Sharpe-ratio verdeelt in feite uw rendement door uw risico. Hogere Sharpe-ratio's duiden op betere risicogecorrigeerde rendementen. (We moeten er rekening mee houden dat de Sharpe-ratio niet alleen kan worden gebruikt om portefeuilles te vergelijken, maar ook om individuele beleggingen zoals beleggingsfondsen en ETF's te vergelijken.)
Om de Sharpe-ratio echt te begrijpen, moet je de formule kennen.
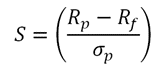
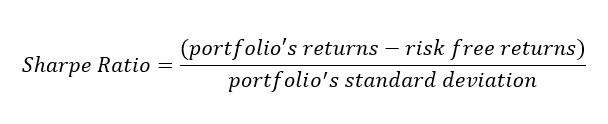
Het lijkt misschien een beetje ingewikkeld, maar de implicaties zijn vrij eenvoudig. Beleggers willen een hoger eigen risico (de bovenste helft van de formule); een hoger getal daar verhoogt de Sharpe-ratio. Maar beleggers willen het risico minimaliseren (weergegeven door standaarddeviatie in de onderste helft van de formule); wanneer het risicogetal hoger wordt, wordt de Sharpe-ratio verlaagd.
Het berekenen van de Sharpe-ratio voor een portfolio is op zichzelf niet erg handig; het is echt bedoeld om de ene portefeuille (of investering) met de andere te vergelijken. De portefeuille met de hogere Sharpe Ratio-score belegt over het algemeen efficiënter voor een bepaald risiconiveau.
Laten we eens kijken naar twee voorbeelden om dit beter te begrijpen. Ten eerste:drie portefeuilles met hetzelfde niveau van volatiliteitsrisico - de standaarddeviatie voor elk is 15% - maar verschillende rendementen. Merk op hoe de variërende opbrengsten de Sharpe-ratio beïnvloeden.
0
Portefeuillerendement:3%
Risicovrij tarief:3%
Standaarddeviatie:15%
0,27
Portefeuillerendement:7%
Risicovrij tarief:3%
Standaarddeviatie:15%
0.80
Portefeuillerendement:15%
Risicovrij tarief:3%
Standaarddeviatie:15%
Portefeuille 1 genereert hetzelfde rendement als een hypothetisch risicovrij actief, maar neemt daarvoor risico's, wat niet efficiënt is; de Sharpe-ratio is 0. Portefeuilles 2 en 3 behalen wat extra rendement, maar als al het andere gelijk is, is Portefeuille 3 superieur - en heeft een hogere Sharpe-ratio - omdat het hogere rendementen genereert zonder extra risico.
Laten we eens kijken naar een tweede voorbeeld waarbij de portefeuilles hetzelfde rendement hebben maar verschillende niveaus van volatiliteitsrisico. Nu verandert de Sharpe-ratio naarmate het risico verandert.
3
Portefeuillerendement:15%
Risicovrij tarief:3%
Standaarddeviatie:4%
0.80
Portefeuillerendement:15%
Risicovrij tarief:3%
Standaarddeviatie:15%
0.34
Portefeuillerendement:15%
Risicovrij tarief:3%
Standaardafwijking:35%
In dit scenario heeft Portfolio 1 de hoogste Sharpe-ratio. Het is superieur aan Portefeuilles 2 en 3 omdat het gelijke rendementen behaalt zonder zoveel risico te nemen. Naarmate de standaarddeviatie (risico) toeneemt, dalen de Sharpe Ratio-scores.
De berekening van de Sharpe-ratio gaat ervan uit dat het rendement van een portefeuille een zogenaamde "normale verdeling" heeft. Maar de aandelenmarkt volgt niet altijd een normale verdeling, wat kan leiden tot tekortkomingen bij de berekening van de standaarddeviatie van een portefeuille. Dat kan op zijn beurt de Sharpe-ratio afwerpen. Dit is over het algemeen minder een probleem bij het vergelijken van goed gespreide portefeuilles versus portefeuilles met slechts een paar aandelen.
Het is ook belangrijk om in gedachten te houden dat het volatiliteitsrisico slechts een van de factoren is waarmee een belegger rekening moet houden bij het beheren van een portefeuille of het evalueren van potentiële beleggingen in aandelen, obligaties, ETF's of beleggingsfondsen.
Het is gemakkelijk om u te concentreren op het beleggingsrendement en geen rekening te houden met risico's bij het analyseren van de prestaties van uw portefeuille of het nemen van investeringsbeslissingen. De Sharpe-ratio is een hulpmiddel dat u mogelijk extra inzicht geeft in de afwegingen tussen risico en rendement. En het is een cijfer waarnaar u misschien wilt zoeken bij het onderzoeken en vergelijken van potentiële beleggingen zoals beleggingsfondsen en ETF's.
Gebruik onze interactieve grafieken om uw rendementspercentages over verschillende tijdsperioden te bekijken en uw portefeuille te vergelijken met meerdere benchmarks.
Ga naar Prestaties en Waarde arrow_forward
(inloggen vereist)
Profiteer van professioneel geldbeheer met beheerde portefeuilles. We helpen u een op maat gemaakte portfolio samen te stellen om u te helpen uw doelen te bereiken en deze vervolgens te beheren om u op het goede spoor te houden.
Meer informatie arrow_forward
De voor- en nadelen van EBITDA begrijpen
Wat is de formule voor de huidige ratio van de balans?
Inzicht in de Fed en rentetarieven
Het Marubozu Candlestick-patroon begrijpen
De verschillende soorten forexhandel begrijpen
De nuances van het Three Drives-patroon begrijpen
De 4 basiselementen van voorraadwaardering