De Sharpe-ratio is een van de risicogecorrigeerde rendementsmethoden die wordt gebruikt bij het evalueren van financiële beleggingen. De ratio is gemaakt door William Sharpe en vertelt ons hoeveel een beleggingsinstrument ons compenseert voor het risico dat het neemt.

Simpel gezegd, het leven is goed zonder risico. U en ik kunnen veilig beleggen in een staatsobligatie, een bank-FD of een PPF en alle volatiliteit en marktruis negeren.

Maar zal het dan voldoende zijn om ons te helpen onze financiële doelen te bereiken?

Dat is wat ons drijft om marktgebonden investeringen na te streven, de volatiliteit te omarmen en hogere rendementen te zoeken dan de veilige havens die we al kennen.

De vraag die daarbij opkomt is echter of het risico dat je neemt voldoende wordt beloond. Wordt u goed gecompenseerd voor het risico dat u neemt?

Of beter, tussen twee marktgebonden beleggingen (zeg uw beleggingsfondsen), welke biedt u een beter rendement voor het genomen risico?

Al deze vragen worden zogenaamd beantwoord door Sharpe Ratio.

En het doet het door een eenvoudige berekening te gebruiken.

Scherpe verhouding =(Totaal rendement van de investering / portefeuille – Risicovrij rendement) / (Standaardafwijking)

De vergelijking spreekt voor zich.

Je kijkt eerst hoeveel excess terug heb je verdiend ten opzichte van het risicovrije rendement. Het risicovrije rendement is doorgaans een rendement op staatsobligaties, dat momenteel rond de 6% ligt. Misschien wilt u hiervoor ook een Bank FD of een PPF-aangifte gebruiken.

Vervolgens deelt u dit extra rendement door de volatiliteit van de marktgebonden belegging die u heeft gedaan. Deze volatiliteit wordt gemeten met behulp van Standaarddeviatie , een van de meest gebruikte tools om dit te doen.

De standaarddeviatie houdt rekening met alle waarden van de investering (zeg de dagelijkse NAV's van de beleggingsfondsen over de afgelopen 3 jaar), berekent een gemiddelde van deze waarden en ontdekt vervolgens de variatie rond het gemiddelde of gemiddelde.

Bereken het getal en je hebt de Sharpe-ratio. Doe het voor een paar extra en je kunt een vergelijkende analyse van de investeringen doen en beslissen welke het meest logisch is.

Heel eenvoudig, toch.

En daar zit de fout.

De standaarddeviatie of volatiliteit hangt af van een zeer fundamentele veronderstelling dat alle marktbewegingen een normale verdeling rond een gemiddelde volgen, wat resulteert in een klokcurve.

Een belcurve ziet eruit als de onderstaande afbeelding. De middelste zwarte lijn is het gemiddelde en alle resultaten vallen aan beide kanten.

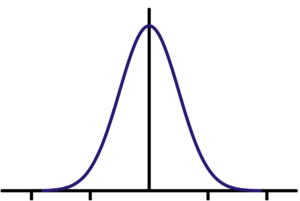
Afbeeldingsbron

Niets is minder waar. Het leven en de markten zijn veel rommeliger.

De belcurve of normale verdeling is gebrekkig omdat het een basisfeit negeert. De grote veranderingen in de markten zijn het gevolg van grote bewegingen (stijging – 2017 of crash – 2008). De markten bewegen misschien voor een lange tijd niet, blijven vlak en dan kunnen we plotseling een enorme stijging zien.

Als alternatief kan er een grote negatieve gebeurtenis zijn, een zwarte zwaan, die de markten in een diep dal zou kunnen duwen.

Aangezien deze gebeurtenissen zeldzaam zijn, wordt er onvoldoende rekening mee gehouden bij het gebruik van berekeningen op basis van een gemiddelde. Hetzelfde geldt voor de meeste risicomaatregelen.

Dus, wat doe je? Neem ten eerste verhoudingen zoals Sharpe Ratio met een korreltje zout.

Het volgende is het ontwikkelen van een beter begrip van risico's.

Hoe?

We zullen het in verdere berichten onderzoeken.

Wat stelt u voor dat een belegger kan doen om risico's beter te begrijpen?