Ten eerste is de enige zekerheid dat er geen zekerheid is. Ten tweede is elke beslissing als gevolg een kwestie van kansenafweging. Ten derde moeten we ondanks onzekerheid beslissen en handelen. En tot slot moeten we beslissingen niet alleen beoordelen op de resultaten, maar ook op de manier waarop die beslissingen zijn genomen.– Robert E. Rubin
Een van de belangrijkste en meest uitdagende aspecten van prognoses is het omgaan met de onzekerheid die inherent is aan het onderzoeken van de toekomst. Ik heb sinds 2003 honderden financiële en operationele modellen gebouwd en ingevuld voor LBO's, fondsenwerving voor startups, budgetten, fusies en overnames en strategische plannen van bedrijven. Ik ben getuige geweest van een breed scala aan benaderingen om dit te doen. Elke CEO, CFO, bestuurslid, investeerder of lid van het investeringscomité brengt zijn eigen ervaring en benadering van financiële projecties en onzekerheid mee, beïnvloed door verschillende prikkels. Vaak geeft het vergelijken van werkelijke resultaten met projecties een waardering voor hoe groot de afwijkingen tussen prognoses en werkelijke resultaten kunnen zijn, en daarom de noodzaak om onzekerheid te begrijpen en expliciet te erkennen.
Ik begon aanvankelijk met het gebruik van scenario- en gevoeligheidsanalyses om onzekerheid te modelleren, en beschouw ze nog steeds als zeer nuttige hulpmiddelen. Sinds ik Monte Carlo-simulaties in 2010 aan mijn gereedschapskist heb toegevoegd, heb ik ontdekt dat ze een uiterst effectief hulpmiddel zijn om de manier waarop u over risico's en kansen denkt te verfijnen en te verbeteren. Ik heb de aanpak voor alles gebruikt, van het opstellen van DCF-waarderingen, het waarderen van call-opties bij fusies en overnames en het bespreken van risico's met kredietverstrekkers tot het zoeken naar financiering en het begeleiden van de toewijzing van VC-financiering voor startups. De aanpak is altijd goed ontvangen door bestuursleden, investeerders en senior managementteams. In dit artikel geef ik een stapsgewijze zelfstudie over het gebruik van Monte Carlo-simulaties in de praktijk door een DCF-waarderingsmodel te bouwen.
Laten we, voordat we met de casestudy beginnen, een paar verschillende benaderingen bekijken om met onzekerheid om te gaan. Het concept van verwachte waarde - het waarschijnlijkheidsgewogen gemiddelde van kasstromen in alle mogelijke scenario's - is Finance 101. Maar financiële professionals, en besluitvormers in het algemeen, hanteren heel verschillende benaderingen bij het vertalen van dit eenvoudige inzicht naar de praktijk. De aanpak kan variëren van het simpelweg niet herkennen of bespreken van onzekerheid aan de ene kant tot geavanceerde modellen en software aan de andere kant. In sommige gevallen besteden mensen uiteindelijk meer tijd aan het bespreken van kansen dan aan het berekenen van cashflows.
Laten we, afgezien van het simpelweg niet aanpakken ervan, eens kijken naar enkele manieren om met onzekerheid om te gaan in projecties op middellange of lange termijn. Veel hiervan zullen u bekend voorkomen.
Eén scenario maken. Deze aanpak is de standaard voor budgetten, veel startups en zelfs investeringsbeslissingen. Behalve dat het geen informatie bevat over de mate van onzekerheid of erkenning dat uitkomsten kunnen verschillen van de projecties, kan het ambigu zijn en verschillend worden geïnterpreteerd volgens de belanghebbende. Sommigen interpreteren het misschien als een rekdoel, waarbij de werkelijke uitkomst eerder tekortschiet dan overschrijdt. Sommigen zien het als een basisprestatie met meer opwaarts dan nadeel. Anderen zien het misschien als een "basisgeval" met een kans van 50/50 op en neer. In sommige benaderingen, vooral voor startups, is het zeer ambitieus en is mislukking of tekort verreweg de meest waarschijnlijke uitkomst, maar een hogere disconteringsvoet wordt gebruikt in een poging om het risico te verantwoorden.
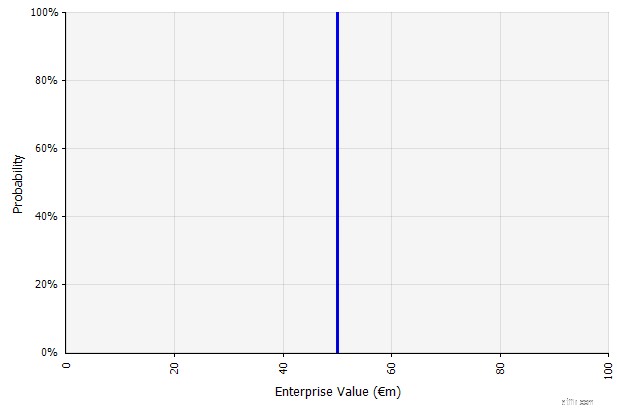
De inputs in de langetermijnkasstroomprognose volgens deze benadering zijn allemaal puntschattingen, wat in dit voorbeeld een puntschattingsresultaat van € 50 miljoen oplevert, met een impliciete waarschijnlijkheid van 100%.
Meerdere scenario's maken. Deze benadering erkent dat het onwaarschijnlijk is dat de werkelijkheid zich volgens een bepaald plan zal ontvouwen.
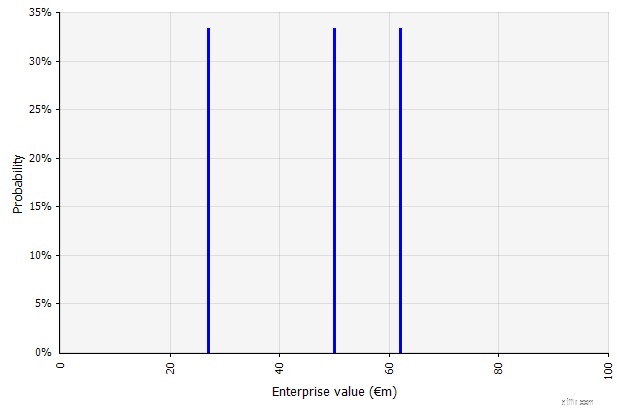
De drie verschillende scenario's leveren drie verschillende resultaten op, waarvan hier wordt aangenomen dat ze even waarschijnlijk zijn. Er wordt geen rekening gehouden met de kansen op uitkomsten buiten de hoge en lage scenario's.
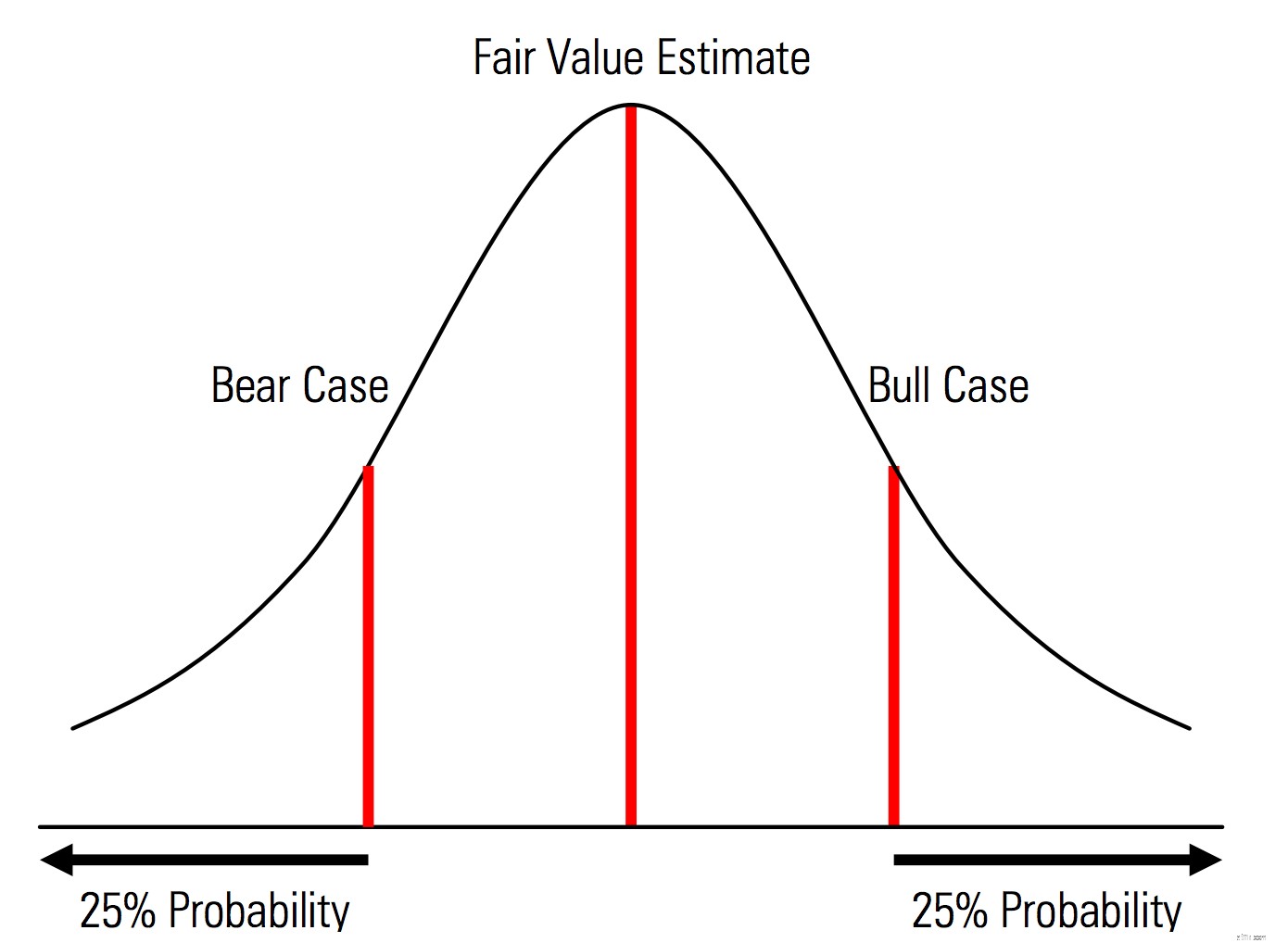
Creëren van basis-, opwaartse en neerwaartse gevallen met kansen die expliciet worden erkend. Dat wil zeggen, de bear- en bull-cases bevatten bijvoorbeeld een waarschijnlijkheid van 25% in elke staart, en de schatting van de reële waarde vertegenwoordigt het middelpunt. Een nuttig voordeel hiervan vanuit het perspectief van risicobeheer is de expliciete analyse van het staartrisico, d.w.z. gebeurtenissen buiten de opwaartse en neerwaartse scenario's.
Illustratie uit het Morningstar Valuation Handbook
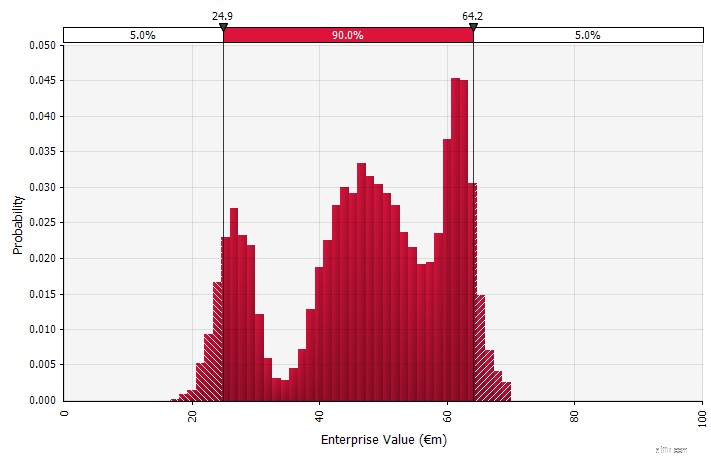
Gebruik van kansverdelingen en Monte Carlo-simulaties. Door kansverdelingen te gebruiken, kunt u het volledige scala aan mogelijke uitkomsten in de prognose modelleren en visualiseren. Dit kan niet alleen op geaggregeerd niveau worden gedaan, maar ook voor gedetailleerde individuele inputs, aannames en drivers. Monte Carlo-methoden worden vervolgens gebruikt om de resulterende kansverdelingen op geaggregeerd niveau te berekenen, waardoor kan worden geanalyseerd hoe verschillende onzekere variabelen bijdragen aan de onzekerheid van de algemene resultaten. Misschien wel het belangrijkste is dat de aanpak iedereen die betrokken is bij de analyse en beslissing dwingt om de onzekerheid die inherent is aan voorspellingen expliciet te erkennen en in waarschijnlijkheden te denken.
Net als de andere benaderingen heeft dit zijn nadelen, waaronder het risico van valse precisie en resulterende overmoed die gepaard kan gaan met het gebruik van een meer geavanceerd model, en het extra werk dat nodig is om geschikte kansverdelingen te selecteren en hun parameters te schatten waar anders alleen puntschattingen zouden zijn gebruikt.
Monte Carlo-simulaties modelleren de waarschijnlijkheid van verschillende uitkomsten in financiële prognoses en schattingen. Ze verdienen hun naam aan het gebied van Monte Carlo in Monaco, dat wereldberoemd is om zijn high-end casino's; willekeurige uitkomsten staan centraal bij de techniek, net als bij roulette en gokautomaten. Monte Carlo-simulaties zijn nuttig in een breed scala van gebieden, waaronder engineering, projectbeheer, olie- en gasexploratie en andere kapitaalintensieve industrieën, R&D en verzekeringen; hier concentreer ik me op toepassingen in financiën en zaken.
In de simulatie worden de onzekere inputs beschreven met behulp van kansverdelingen, beschreven door parameters zoals gemiddelde en standaarddeviatie. Voorbeeldinvoer in financiële projecties kan van alles zijn, van inkomsten en marges tot iets meer gedetailleerd, zoals grondstofprijzen, kapitaaluitgaven voor een uitbreiding of wisselkoersen.
Wanneer een of meer inputs worden beschreven als kansverdelingen, wordt de output ook een kansverdeling. Een computer trekt willekeurig een getal uit elke invoerverdeling en berekent en slaat het resultaat op. Dit wordt honderden, duizenden of tienduizenden keren herhaald, elk een iteratie genoemd. Wanneer ze samen worden genomen, benaderen deze iteraties de kansverdeling van het uiteindelijke resultaat.
De invoerverdelingen kunnen ofwel continu . zijn , waarbij de willekeurig gegenereerde waarde elke waarde onder de verdeling kan aannemen (bijvoorbeeld een normale verdeling), of discreet , waar waarschijnlijkheden zijn gekoppeld aan twee of meer verschillende scenario's.
Een simulatie kan ook een mix van distributies van verschillende typen bevatten. Neem bijvoorbeeld een farmaceutisch R&D-project met verschillende fasen die elk een discrete kans op succes of mislukking hebben. Dit kan worden gecombineerd met doorlopende distributies die de onzekere investeringsbedragen beschrijven die nodig zijn voor elke fase en potentiële inkomsten als het project resulteert in een product dat op de markt komt. De onderstaande grafiek toont de output van een dergelijke simulatie:een kans van ~65% om de gehele investering van € 5 miljoen tot € 50 miljoen (contante waarde) te verliezen, en een kans van ~35% op een nettowinst die hoogstwaarschijnlijk in het bereik van € 100 tot € 250 – informatie die verloren zou gaan als belangrijke outputstatistieken zoals MIRR of NPV worden weergegeven als puntschattingen in plaats van kansverdelingen.
Voorbeeld Monte Carlo-simulatie voor een project met verschillende go/no-go-fasen en onzekere investeringen ertussen, met onzekere waarde als het project wordt voltooid
Een van de redenen waarom Monte Carlo-simulaties niet op grotere schaal worden gebruikt, is omdat de typische dagelijkse financiële tools ze niet zo goed ondersteunen. Excel en Google Spreadsheets bevatten één getal of formuleresultaat in elke cel, en hoewel ze kansverdelingen kunnen definiëren en willekeurige getallen kunnen genereren, is het omslachtig om vanaf het begin een financieel model met Monte Carlo-functionaliteit te bouwen. En hoewel veel financiële instellingen en beleggingsondernemingen Monte Carlo-simulaties gebruiken voor het waarderen van derivaten, het analyseren van portefeuilles en meer, zijn hun tools doorgaans intern ontwikkeld, eigendom van eigendom of onbetaalbaar, waardoor ze ontoegankelijk zijn voor de individuele financiële professional.
Daarom wil ik de aandacht vestigen op Excel-plug-ins zoals @RISK van Palisade, ModelRisk van Vose en RiskAMP, die het werken met Monte Carlo-simulaties aanzienlijk vereenvoudigen en u in staat stellen ze te integreren in uw bestaande modellen. In de volgende uitleg zal ik @RISK gebruiken.
Laten we een eenvoudig voorbeeld bekijken dat de belangrijkste concepten van een Monte Carlo-simulatie illustreert:een kasstroomprognose voor vijf jaar. In deze walkthrough heb ik een basiskasstroommodel voor waarderingsdoeleinden opgezet en ingevuld, de invoer geleidelijk vervangen door kansverdelingen en ten slotte de simulatie uitgevoerd en de resultaten geanalyseerd.
Om te beginnen gebruik ik een eenvoudig model, gericht op het benadrukken van de belangrijkste kenmerken van het gebruik van kansverdelingen. Merk op dat dit model om te beginnen niet verschilt van enig ander Excel-model; de plug-ins die ik hierboven noemde werken met uw bestaande modellen en spreadsheets. Het onderstaande model is een eenvoudige kant-en-klare versie gevuld met aannames om één scenario te vormen.
Eerst moeten we de informatie verzamelen die nodig is om onze aannames te doen, daarna moeten we de juiste kansverdelingen kiezen om in te voegen. Het is belangrijk op te merken dat de bron van de belangrijkste inputs/aannames hetzelfde is, ongeacht welke benadering u kiest om met onzekerheid om te gaan. Commerciële due diligence, een uitgebreide beoordeling van het bedrijfsplan van het bedrijf in de context van verwachte marktontwikkeling, branchetrends en concurrentiedynamiek, omvat doorgaans extrapolatie van historische gegevens, het opnemen van deskundig advies, het uitvoeren van marktonderzoek en het interviewen van marktdeelnemers. In mijn ervaring bespreken experts en marktdeelnemers graag verschillende scenario's, risico's en verschillende uitkomsten. De meeste beschrijven echter niet expliciet kansverdelingen.
Laten we nu onze belangrijkste invoerwaarden één voor één doornemen en vervangen door kansverdelingen, te beginnen met de geschatte omzetgroei voor het eerste prognosejaar (2018). De @RISK-plug-in voor Excel kan worden geëvalueerd met een gratis proefperiode van 15 dagen, zodat u deze met een paar klikken van de Palisade-website kunt downloaden en installeren. Als de @RISK-plug-in is ingeschakeld, selecteert u de cel waarin u de distributie wilt en selecteert u 'Definieer distributie' in het menu.
Vervolgens selecteert u er een uit het palet met distributies dat verschijnt. De @RISK-software biedt meer dan 70 verschillende distributies om uit te kiezen, dus het kiezen ervan kan in het begin overweldigend lijken. Hieronder is een gids voor een handvol die ik het vaakst gebruik:
Normaal. Gedefinieerd door gemiddelde en standaarddeviatie. Dit is een goed startpunt vanwege de eenvoud en geschikt als uitbreiding op de Morningstar-benadering, waarbij u een verdeling definieert die misschien al gedefinieerde scenario's of bereiken voor een bepaalde invoer dekt, en ervoor zorgt dat de gevallen symmetrisch zijn rond het basisscenario en dat de kansen in elke staart redelijk lijken (zeg 25% zoals in het Morningstar-voorbeeld).
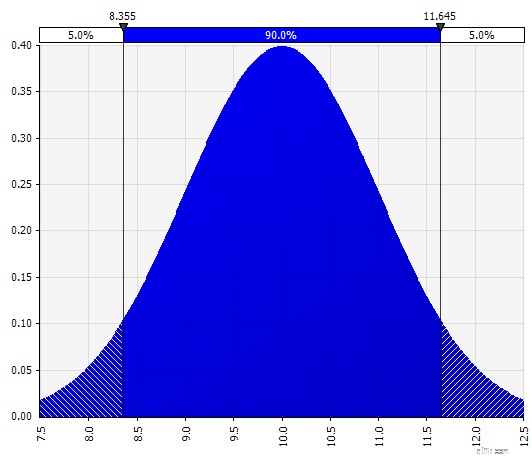
Johnson Moments. Als u dit kiest, kunt u scheve verdelingen en verdelingen met dikkere of dunnere staarten definiëren (technisch toevoegen van scheefheid- en kurtosis-parameters). Achter de schermen gebruikt dit een algoritme om een van de vier distributies te kiezen die de vier gekozen parameters weerspiegelen, maar dat is onzichtbaar voor de gebruiker --- we hoeven ons alleen maar te concentreren op de parameters.
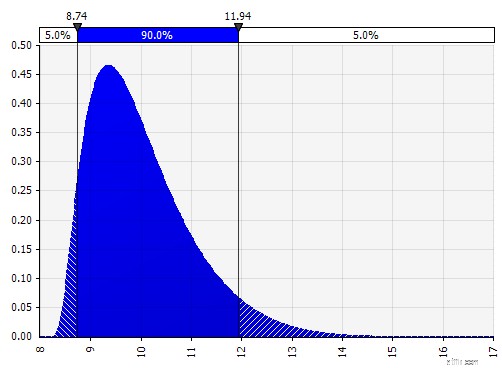
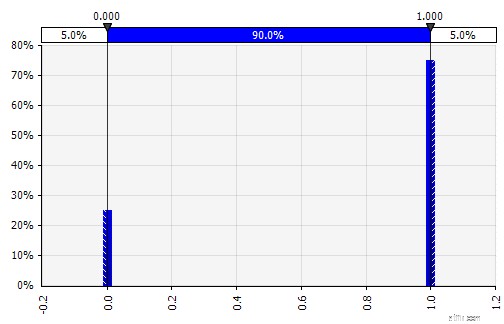
Discreet. Waar kansen worden gegeven aan twee of meer specifieke waarden. Terugkerend naar het voorbeeld van een gefaseerd R&D-project in het begin, wordt de kans op succes in elke fase gemodelleerd als een binaire discrete verdeling, waarbij een uitkomst van 1 staat voor succes en 0 voor mislukking.
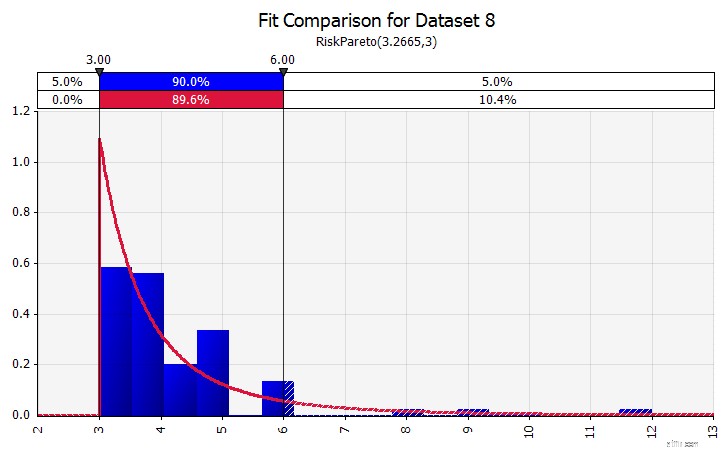
Distributie-aanpassing. Wanneer u een groot aantal historische gegevenspunten heeft, is de functionaliteit voor distributie-aanpassing handig. Dit betekent bijvoorbeeld niet drie of vier jaar historische omzetgroei, maar tijdreeksgegevens zoals grondstofprijzen, valutakoersen of andere marktprijzen waar de geschiedenis nuttige informatie kan geven over toekomstige trends en de mate van onzekerheid.
Verschillende distributies combineren in één.
Om de potentiële impact van individuele vooroordelen te verminderen, is het vaak een goed idee om de input van verschillende bronnen op te nemen in een veronderstelling en/of om de bevindingen te beoordelen en te bespreken. Er zijn verschillende benaderingen:
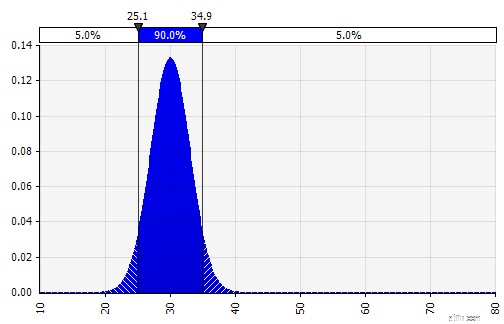
Gewicht:20%
+
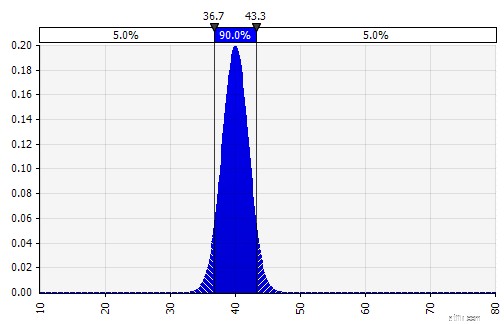
Gewicht:20%
+
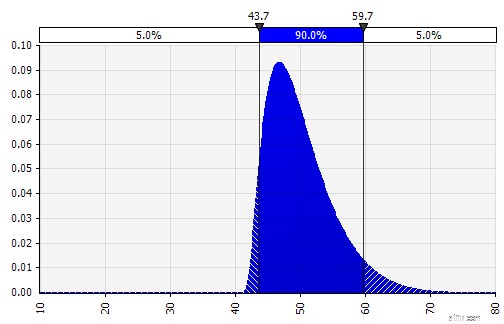
Gewicht:60%
=
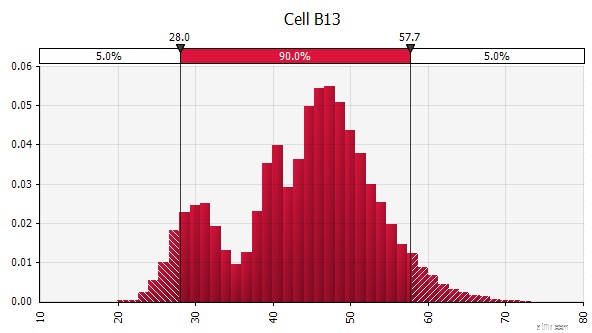
Uit de vrije hand. Om snel een distributie te illustreren als onderdeel van discussies of als u een distributie nodig heeft bij het opstellen van een model dat niet gemakkelijk uit het bestaande palet kan worden gemaakt, is de functionaliteit uit de vrije hand handig. Zoals de naam al aangeeft, kunt u hiermee de verdeling tekenen met een eenvoudig tekengereedschap.
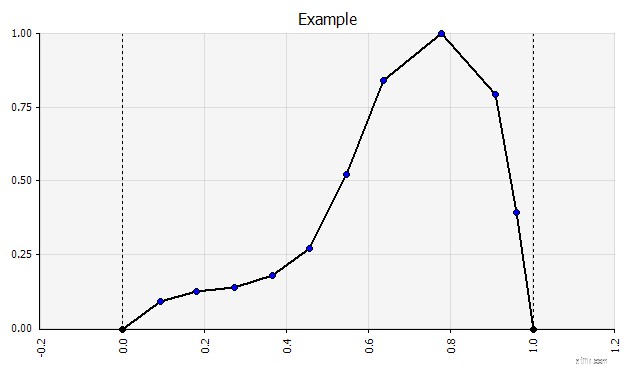
Nu zien we een visualisatie van de verdeling, met een paar parameters aan de linkerkant. De symbolen voor het gemiddelde en de standaarddeviatie moeten er bekend uitzien. In het geval van een normale verdeling zou het gemiddelde zijn wat we eerder als een enkele waarde in de cel hebben ingevoerd. Hier is de verkoopkansverdeling van 2018 als voorbeeld, waarbij 10% het gemiddelde vertegenwoordigt. Terwijl uw typische model zich ofwel alleen zou richten op het cijfer van 10%, ofwel "bull"- en "bear"-scenario's zou hebben met respectievelijk 15% en 5% groei, geeft dit nu informatie over het volledige scala aan verwachte potentiële resultaten.
Waarschijnlijkheidsverdeling van omzetgroei in één jaar
Een voordeel van Monte Carlo-simulaties is dat staartuitkomsten met een lage waarschijnlijkheid tot nadenken en discussies kunnen leiden. Alleen het weergeven van opwaartse en neerwaartse scenario's kan het risico met zich meebrengen dat besluitvormers deze als de buitengrenzen interpreteren en alle scenario's die daarbuiten liggen afwijzen. Dit kan resulteren in gebrekkige besluitvorming, met blootstelling aan resultaten die buiten de risicotolerantie van de organisatie of het individu liggen. Zelfs een kans van 5% of 1% kan onaanvaardbaar zijn als het scenario in kwestie catastrofale gevolgen zou hebben.
Houd er bij Monte Carlo-modellering rekening mee hoe onzekerheid en kansverdelingen op elkaar stapelen, bijvoorbeeld in de loop van de tijd. Laten we een voorbeeld bekijken. Aangezien de verkoop in elk jaar afhankelijk is van de groei in de voorgaande jaren, kunnen we visualiseren en zien dat onze schatting van de verkoop in 2022 onzekerder is dan die voor 2018 (weergegeven met behulp van de standaarddeviaties en 95% betrouwbaarheidsintervallen in elk jaar). Voor de eenvoud specificeert het onderstaande voorbeeld de groei voor één jaar, 2018, en past datzelfde groeipercentage vervolgens toe op elk van de volgende jaren tot 2022. Een andere benadering is om vijf onafhankelijke distributies te hebben, één voor elk jaar.
Illustreren hoe de onzekerheid in de loop van de tijd toeneemt (verbreding van de verdeling van resultaten)
We schatten nu een kansverdeling voor de EBIT-marge in 2018 (hieronder gemarkeerd) op dezelfde manier als hoe we het deden voor omzetgroei.
Hier kunnen we de correlatiefunctie gebruiken om een situatie te simuleren waarin er een duidelijke correlatie is tussen relatief marktaandeel en winstgevendheid, wat schaalvoordelen weerspiegelt. Scenario's met een hogere omzetgroei ten opzichte van de markt en een overeenkomstig hoger relatief marktaandeel kunnen worden gemodelleerd om een positieve correlatie te hebben met hogere EBIT-marges. In sectoren waar het vermogen van een bedrijf sterk gecorreleerd is met een andere externe factor, zoals olieprijzen of wisselkoersen, kan het zinvol zijn om een verdeling voor die factor te definiëren en een correlatie met verkoop en winstgevendheid te modelleren.
Modellering van correlatie tussen omzetgroei en marges
Afhankelijk van de beschikbare tijd, de omvang van de transactie en andere factoren, is het vaak zinvol om een bedrijfsmodel te bouwen en de meest onzekere variabelen expliciet in te voeren. Deze omvatten:productvolumes en prijzen, grondstofprijzen, wisselkoersen, belangrijke overheadposten, maandelijks actieve gebruikers en gemiddelde opbrengst per eenheid (ARPU). Het is ook mogelijk om modellen te modelleren die verder gaan dan de hoeveelheidsvariabelen, zoals ontwikkelingstijd, time-to-market of marktacceptatiegraad.
Met behulp van de geschetste aanpak kunnen we nu doorgaan met de balans en het kasstroomoverzicht, vullen met veronderstellingen en kansverdelingen gebruiken waar dit zinvol is.
Een opmerking over capex:dit kan worden gemodelleerd in absolute bedragen of als percentage van de omzet, mogelijk in combinatie met grotere stapsgewijze investeringen; een productiefaciliteit kan bijvoorbeeld een duidelijke capaciteitslimiet hebben en een grote uitbreidingsinvestering of een nieuwe faciliteit die nodig is wanneer de verkoop de drempel overschrijdt. Aangezien elk van de zeg maar 1.000 of 10.000 iteraties een volledige herberekening van het model zal zijn, kan een eenvoudige formule worden gebruikt die de investeringskosten activeert als/wanneer een bepaald volume wordt bereikt.
Het bouwen van een Monte Carlo-model heeft één extra stap in vergelijking met een standaard financieel model:de cellen waar we de resultaten willen evalueren, moeten specifiek worden aangeduid als uitvoercellen. De software slaat de resultaten van elke iteratie van de simulatie op voor die cellen zodat we ze kunnen evalueren nadat de simulatie is voltooid. Alle cellen in het hele model worden bij elke iteratie opnieuw berekend, maar de resultaten van de iteraties in andere cellen, die niet zijn aangewezen als invoer- of uitvoercellen, gaan verloren en kunnen niet worden geanalyseerd nadat de simulatie is voltooid. Zoals je kunt zien in de onderstaande schermafbeelding, wijzen we de MIRR-resultaatcel aan als een uitvoercel.
Als u klaar bent met het bouwen van het model, is het tijd om de simulatie voor de eerste keer uit te voeren door simpelweg op "start simulatie" te drukken en een paar seconden te wachten.
Uitvoer uitgedrukt als kansen. Terwijl ons model ons eerder een enkele waarde voor de gewijzigde IRR gaf, kunnen we nu duidelijk zien dat er een aantal potentiële uitkomsten rond die waarde zijn, met verschillende waarschijnlijkheden. Dit stelt ons in staat om vragen te herformuleren, zoals "Zullen we onze hindernis halen met deze investering?" tot "Hoe waarschijnlijk is het dat we onze drempel zullen halen of overschrijden?" U kunt onderzoeken welke uitkomsten het meest waarschijnlijk zijn met behulp van bijvoorbeeld een betrouwbaarheidsinterval. De visualisatie is handig bij het communiceren van de resultaten aan verschillende belanghebbenden, en u kunt de output van andere transacties over elkaar heen leggen om visueel te vergelijken hoe aantrekkelijk en (on)zeker de huidige is vergeleken met andere (zie hieronder).
Gewijzigde IRR met betrouwbaarheidsintervallen
Gewijzigde IRR met een drempelwaarde
Gewijzigde IRR met andere transacties bedekt
De mate van onzekerheid in het eindresultaat begrijpen. Als we een grafiek van cashflowvariabiliteit in de tijd genereren, vergelijkbaar met wat we aanvankelijk deden voor verkoop, wordt het duidelijk dat de variabiliteit in vrije cashflow significant wordt, zelfs met relatief bescheiden onzekerheid in verkoop en de andere inputs die we hebben gemodelleerd als kansverdelingen , met resultaten variërend van ongeveer € 0,5 miljoen tot € 5,0 miljoen - een factor 10x - zelfs slechts één standaarddeviatie van het gemiddelde. Dit is het resultaat van het op elkaar stapelen van onzekere veronderstellingen, een effect dat zowel 'verticaal' door de jaren heen als 'horizontaal' door de financiële overzichten heen werkt. De visualisaties geven informatie over beide soorten onzekerheid.
Variabiliteit van vrije cashflow in vergelijking met variabiliteit in verkoop
Gevoeligheidsanalyse:introductie van de tornado-grafiek. Een ander belangrijk gebied is om te begrijpen welke input de grootste impact heeft op uw eindresultaat. Een klassiek voorbeeld is hoe het belang van disconteringsvoet- of eindwaarde-aannames vaak te weinig gewicht krijgt ten opzichte van kasstroomprognoses. Een veelgebruikte manier om dit aan te pakken, is door matrices te gebruiken waarbij u één toetsinvoer op elke as plaatst en vervolgens het resultaat in elke cel berekent (zie hieronder). This is useful especially in situations where decisions hinge on one or a few key assumptions—in these “what you have to be believe” situations, decision-makers on (for example) an investment committee or a senior management team may have different views of those key assumptions, and a matrix such as the one above allows each one of them to find a result value corresponding to their view, and can decide, vote, or give advice based on that.
Example Sensitivity Analysis Matrix - Enterprise Value as a Function of the Cost of Capital and Year Five Exit Multiple
Enhancing with Monte Carlo simulations. When using Monte Carlo simulations, that approach can be complemented with another:the tornado diagram. This visualization lists the different uncertain inputs and assumptions on the vertical axis and then shows how large the impact of each is on the end result.
Tornado Diagram Showing Sensitivity to Key Inputs
This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.
Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.
Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb
It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.
In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.
The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.
In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.
There are two concepts here and it is important to separate them:one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it:Monte Carlo simulations in spreadsheets.
I don’t use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.
Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.
I spend 98% of my time on 2% probabilities – Lloyd Blankfein
De taken van de executeur van een nalatenschap uitvoeren
Waarom ik een hekel heb aan Monte Carlo-analyse en andere financiële projecties
Wed niet met pensioen op Monte Carlo-modellen
Wat is kwalitatieve analyse van aandelen? En hoe het uit te voeren?
Uitgelegd:hoe is PESTLE-analyse (met voorbeeld)? Hoe voer je het uit?
DMart-bedrijfsmodel en succesmantra - Hoe verdient DMart geld?
Wat is Portfolio Backtesting? Hoe voer je het uit op Indiase aandelen?